F. Wagner May 2006
StateWORKS:
Lifetime of control signals
and generating events,
illustrated by a Turing machine.
Introduction
A control system reacts to input signals which change in time. A period between two consecutive changes of a signal is defined as its lifetime. Depending on a signal it may be desirable to shorten its lifetime by "consuming" it before the next change occurs.
In most software control systems a change of a signal value generates an event which triggers its processing. In such a system a repetition of the same value usually does not make sense, but it may be required. A similar problem exist for outputs which should be "detected" by the output world if they change.
The life time of control values and generation of input and output events are topics of this technical note. The discussion is supported by an example of a state machine controlling a Turing machine model.
Consuming control values
The state machine behaviour in a given state depends on its inputs. In the VFSM approach the virtual inputs represents the entire input information in form of control values. A control value is entered into the virtual input if a corresponding real input changes. The control values have varied characteristics.
Any input is characterized by a set of control values which are as a rule mutually exclusive ones (at least the RTDB follows this philosophy). For instance, a digital input (object DI in RTDB) have three control values: LOW (representing e.g. DoorOpen), HIGH (representing e.g. DoorClosed) and UNKNOWN (representing e.g. DoorPositionUnknown). The virtual input contains always one of those values. Any value can be replaced by another value of that set: it happens only if the real input changes. We may say that the life time of a such a control value is determined by the duration of the real input value.
Another input type represents a command (object CMD in the RTDB) which has several control values corresponding to numbers representing commands, for instance: 1 (representing e.g. CmdStart), 2 (representing e.g. CmdStop), 3 (representing e.g. CmdContinue), 4 (representing e.g. CmdStep). The virtual input may contain one of those values. Any value can be replaced by another value of that set if the command changes. In addition, a command control value may be explicitly removed (using the output action MyCmd_Clear) from the virtual input. Actually, a command is given a null value to clear it. This situation means that the last command has lost its meaning but no new command has been issued yet.
An extreme type represent inputs for which the control values are consumed (removed or replaced by another value) if once used. Strings in parsers are examples of such inputs. In the RTDB the object PAR performs a change from CHANGED to DEF if used. Another object - STR - becomes effectively disabled in MATCH and NOMATCH states and must be enabled by forcing a change to the state SET.
Another case represents the object XDA which is most often used (and sometimes also misused) for inputs which are consumed. Therefore we shall discuss its use in more detail. The object XDA is similar to an object CMD but without its restrictions (use limited to the Master-Slave interface). The object XDA is an unsigned integer and may be used to represent input signals as well as output signals. This explains its value in cases where a designer has to decide about the life time of control signals created on XDA values. Consuming an XDA control value means to define an (output) action which sets it to a neutral value not used for creation of some other control value. For instance, we use (taken from the example below) MoveDone (1) as a control value. Using an action ClearMoveDone to set the XDA value to 0 effectively removes the XDA control value from the virtual input.
Generating input events
The VFSM executor is triggered by events. An event is caused by a change of a control value. There are objects which changes are clear, and mean e.g. for a digital output one of the following: LOW->HIGH, LOW->UNKNOWN, HIGH->LOW, etc.; a change LOW->LOW does not make sense.
The problem is not so obvious for certain other objects which behave like a command: in addition to change like CmdStart->CmdStop we may want to repeat the command. Repeating the command would mean to apply for instance the CmdStep several times in succession. Unfortunately, receiving the same command value means no change for the command object. In such situations we have to force an intermediate dummy change, regenerating in such a way the ability of the object to create an event. For the CMD object a special Clear action is available.
Another object often used for this purpose is XDA. It is an input/output object and if used as an input object it needs also one dummy value as an action. Those dummy value is then used as a "break" between two identical input values.
Output action events
A different life time problem exists for outputs which are defined by objects used for defining actions. Performing an action means to trigger an I/O handler which is to pass a real value to the controlled application. This can be repeated at any time. If the TCP/IP communication is used for that purpose clients are advised only if an object value has changed. Performing the same action means setting the same value and does not generate an event which would be sent to clients. Hence, any outputs controlled via TCP/IP link cannot repeat the same value. Of course, if the value is a digital output there is no use for repeating its value. If the output has a "command" character (do something) we may want to repeat an action, for instance repeating several movements in the same direction. Such application requires interleaving two identical actions with dummy actions (do nothing) which effectively produces the required events.
As already mentioned string processing is an extreme example of events which as a rule have to be consumed immediately after they are used. Therefore we have chosen a Turing machine as an example supporting our discussion. In that example we will be able to show all discussed problems: consumption of used (input) control values, regeneration of the event creation ability of input objects and generation of (output) events for repeated actions. The reader may download the example and study it by using StateWORKS Studio.
Turing machine
A Turing machine [1] consists of a tape and a read/write head. The head can be moved along the tape (or tape in relation to the head) to the right or left. The head can read a symbol from the tape and can write a symbol onto the tape.
The functioning of the Turing machine is determined by a finite state machine which reacts to symbols scanned by the head. After each movement the head reads a symbol from the tape. Depending on the read symbol the finite state machine decides what to do:
- leave the symbol on the type or overwrite it with another symbol
- move to the right or to the left
A Turing machine does not have any practical meaning but it is a good conceptual model for the study of automata.
Turing machine model
We have prepared a model of a Turing machine as shown in Figure 1. The actual model of a Turing machine is a tape represented by 24 cells which can contain digits 0 and 1. The position of the head is indicated as a "grey" cell. Running an appropriate state machine we can solve a specific problem with the Turing machine. The state machine controls the head movements and the writing of symbols onto the tape.

The full graphical user interface of the model is shown in Figure 2. The model connects to the RTDB based StateWORKS run-time system (for instance SWLab) running a state machine which is to control the Turing machine. The upper part of the model displays information about the connections (TCP/IP address and port), a list of RTDB objects used and the configuration path of the used state machine. Entering any other symbol is considered as an empty cell. The lower part of the model shows a log windows which display all signals received by the Turing machines. The log window may be cleared.
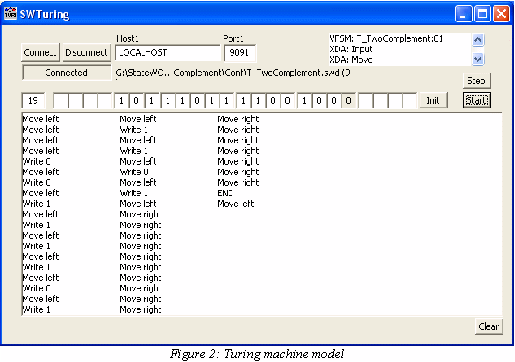
The model employs "advise" on the XDA objects "Move" and "Write" (with attribute .Val). Thus, any changes of those values trigger the Turing machine. The machine can perform two operations:
- Write: 0, 1, 2 ("clear" the cell content) and 4 (END of the operation)
- Move: 0 (move left) and 1 (move right).
The Write operation is acknowledged by a WriteDone signal = 1 (Figure 3a).
The Move operation is acknowledged by a MoveDone signal = 1. In addition, the present input symbol under the head is read and sent to the RTDB setting there the value of the object "Input" (Figure 3b). The Input symbols are limited to:
- 0 and 1 (corresponding to 0 and 1 of the Write symbols)
- any other unsigned integer is interpreted as an empty cell (in the examples the value 2 is used)

Figure 3: Turing machine acknowledges the Write (a) and Move (b) signals
In addition, in the specification of the state machine the value 3 is used for Input as well as for Write for denoting a "none" symbol.
The model of the Turing machine has the following buttons:
- Connect: connects to the StateWORKS run-time system.
- Disconnect: disconnects from the StateWORKS run-time system.
- Init: initializes the cell to a predefined string (defined by the objects Par:InitString, Par:Begin StringPos and Par:StartPos). The string length is limited to 24 characters. The string and the start position can be also entered manually.
- Start/Stop: starts and stop the processing of the tape.
- Step: realizes one processing step.
- Clear: clears the content of the log window.
Analysis of the example
Any Turing machine using the binary alphabet {0,1} can be realized and studied using the software model. We have prepared an example which calculates a two's complement of a binary number using the known algorithm: check the digits from the right-most position, leaving them unchanged until meeting a "1". Leave the first "1" encountered unchanged and continue checking by inverting all subsequent digits. The initialisation values are:
Par:InitString = 0100010000111000
Par:Begin StringPos =
4
Par:StartPos = 19
where the parameter Par:InitString defines the 16-bit binary number to be converted into a two's complement.
The state transition diagram of the state machine which controls the Turing machine and realizes the conversion is shown in Figure 4. The processing of the binary number has three phases:
- Moving to the left until the digit "1" is encountered - realized by states: MoveLeft0 and MoveLeft0Done.
- First digit "1" is skipped (state MoveLeft1) and all following digits are negated - realized by states MoveLeft0Done, Write1_MoveLeft and Write0_MoveLeft.
- Encountering the empty cell terminates the processing and the head returns to the initial (left) position - realized by states: MoveRight and MoveRightDone; the initial position is identified when the head detects an empty cell which causes the last movement to the left (state MoveLeft).

Figure 4: The ST diagram of the T_TwoComplement state machine
The details of the solution can be studied in the project T_TwoComplement.prj. Running the application using SWLab we can test it more carefully changing the binary number and running the conversion continuously (Start/Stop button) or step-by-step (Step button). The log window shows all (Move and Write) commands send to the Turing machine models.
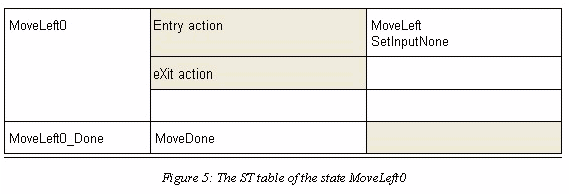
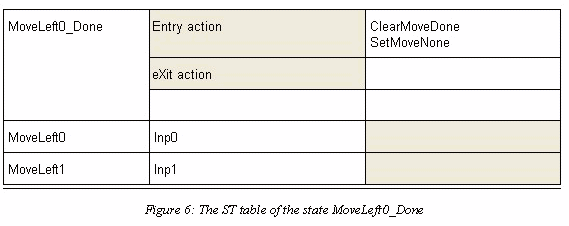
We will limit the discussion to an analysis of the states which show solutions of the problems discussed in the beginning: consumption of control values and generation of input and output events. We take for that two states shown in Figure 5 and Figure 6.On entering the state MoveLeft0 the state machine issues the output MoveLeft and waits for an acknowledgement. Receiving the acknowledgement MoveDone the state machine goes to the state MoveLeft0_Done where it clears the MoveDone control value.
In both states dummy actions are performed allowing objects to generate an event:
- The action SetMoveNone in the state MoveLeft0Done allows a repetition of the action MoveLeft after return to the state MoveLeft0.
- The action SetInputNone in the state MoveLeft0 assure an input event in the state MoveLeft0_Done.
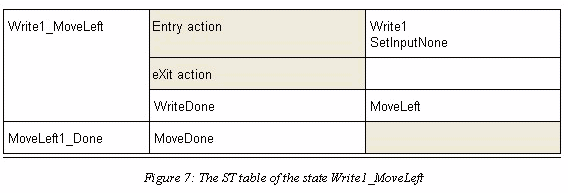
The state machine sends to the Turing machine either a Move signal or Move and Write signals. In the later case the sequence Move-Write must be assured. Instead of using two states we have arranged it as shown in Figure 7. On entering the state Write1_MoveLeft the state machine sends the signal Write1 to the Turing machine. Receiving the acknowledgement WriteDone the state machine sends the signal MoveLeft (as an Input Action). If this signal is acknowledged by the MoveDone signal the state machine changes to the state MoveLeft1_Done.
Conclusions
When coding a parser type of application we use events to trigger a function which processes the corresponding string or message. Executing directly the specification with the help of the StateWORKS run-time system we have to handle explicitly the consumption of events and regeneration of event creation. Though parser type of problems are rather rare in some environments (such as industrial control) the RTDB allows us to efficiently handle such problems.
The model of a Turing machine created for the purpose of this note may be used for studying Turing exercises defined for a binary alphabet {0, 1}. By specifying an appropriate state machine we may solve and test any problem in that range.
References
[1] Caroll J., Long D., Theory of Finite Automata, Prentice Hall, New Jersey, 1989.
[2] Wagner, F. et al., Modeling Software with Finite State Machines - A Practical Approach, Auerbach Publications, New York, 2006.

 download PDF version
download PDF version